Pierre de Fermat (Beaumont-de-Lomagne, Francia, 17 de agosto de 1601;1 Castres, Francia, 12 de enero de 1665) fue un jurista y matemático francés apodado por Eric Temple Bell con el sobrenombre de «príncipe de los aficionados».2
Fermat fue junto con René Descartes uno de los principales matemáticos de la primera mitad del siglo XVII.
Descubrió el cálculo diferencial antes que Newton y Leibniz, fue co-fundador de la teoría de probabilidades junto a Blaise Pascal e independientemente de Descartes, descubrió el principio fundamental de la geometría analítica. Sin embargo, es más conocido por sus aportaciones a la teoría de números en especial por el conocido como último teorema de Fermat, que preocupó a los matemáticos durante aproximadamente 350 años, hasta que fue demostrado en 1995 por Andrew Wiles ayudado por Richard Taylor.
Fermat es uno de los pocos matemáticos que cuentan con un asteroide con su nombre, (12007) Fermat. También se le ha dado la denominación de Fermat a un cráter lunar de 39 km de diámetro.
Biografía
La mansión del siglo XV donde nació es en la actualidad un museo. La escuela más antigua y prestigiosa de Toulouse se llama Pierre de Fermat y en ella se imparten clases de ingeniería y comercio. Está situada entre las diez mejores de Francia para clases preparatorias. Cabe destacar que Fermat estudió y analizó las matemáticas en sus tiempos libres ya que él tenía otra profesión.Obra matemática
Espiral de Fermat
También conocida como espiral parabólica, es una curva que responde a la siguiente ecuación:Números amigos
Dos números amigos son dos números naturales a y b tales que a es la suma de los divisores propios de b y b es la suma de los divisores propios de a. (la unidad se considera divisor propio, pero no lo es el mismo número).En 1636, Fermat descubrió que 17.296 y 18.416 eran una pareja de números amigos, además de redescubrir una fórmula general para calcularlos, conocida por Tabit ibn Qurra, alrededor del año 850.
Números primos
Un número de Fermat es un número natural de la forma:[editar] Teorema sobre la suma de dos cuadrados
El teorema sobre la suma de dos cuadrados afirma que todo número primo p, tal que p-1 es divisible entre 4, se puede escribir como suma de dos cuadrados. El 2 también se incluye, ya que 12+12=2. Fermat anunció su teorema en una carta a Marin Mersenne fechada el 25 de diciembre de 1640, razón por la cual se le conoce también como Teorema de navidad de FermatPequeño teorema de Fermat
El pequeño teorema de Fermat, referente a la divisibilidad de números, afirma que, si se eleva un número a a la p-ésima potencia y al resultado se le resta a, lo que queda es divisible por p, siendo p un número primo. Su interés principal está en su aplicación al problema de la primalidad y en criptografía.Principio de Fermat
Último teorema de Fermat
Pierre de Fermat acostumbraba a escribir las soluciones a los problemas en el margen de los libros. Una de las notas que escribió en su ejemplar del texto griego de La Aritmética de Diofanto (editada por Claude Gaspard Bachet de Méziriac en 1621) lo siguiente:| Cubem autem in duos cubos, aut quadratoquadratorum in duos cuadratosquadratos, et generaliter nullam in infinitum ultra cuadratum potestandem in duos ejusdem nominis dividere: cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exigitas non caparet. | Es imposible encontrar la forma de convertir un cubo en la suma de dos cubos, una potencia cuarta en la suma de dos potencias cuartas, o en general cualquier potencia más alta que el cuadrado en la suma de dos potencias de la misma clase; para este hecho he encontrado una demostración excelente. El margen es demasiado pequeño para que la demostración quepa en él. |
Pierre de Fermat

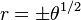
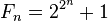

No hay comentarios:
Publicar un comentario